Javascript required
Skip to content Skip to sidebar Skip to footer
Home / Find the Solution Set for the Following Equation

Find the Solution Set for the Following Equation

Solution of Systems of Linear inequalities in One Variable

Sometimes it is necessary to find the common solution, or solution set, of two or more inequalities, called a system of inequalities. The solution set of a system of inequality is thus the intersection of the solution set of each inequality in the system.

EXAMPLE Find the solution set of the following system:

6x+3>=2x-5 and3x-7<5x-9

Solution

We first find the solution set of each inequality.

6x+3>=2x-5 3x-7<5x-9
4x>=-8 92x<-2
x>=-2 x>1

The Solution set is

inequalities

The Solution set is

solution of inequalities

The solution set of the system (Figure 5.7) is

system of inequalities

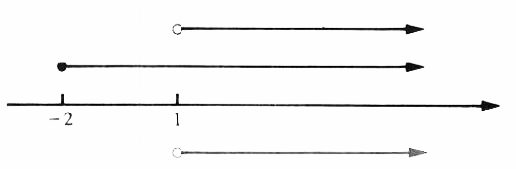
graphical representation for solution set example

FIGURE 5.7

Let's see how our Linear inequalities solversolves this and similar problems. Click on "Solve Similar" button to see more examples.

EXAMPLE Find the solution set of the following system:

4(3-x)<7+3(2-x) and 3(x-1)<4-(1-x)

Solution We first find the solution set of each inequality

4(3-x)<7+3(2-x) 3(x-1)<4-(1-x)
12-4x<7+6-3x 3x-3<4-1+x
-x<1 2x<6
x>-1 x<3

The Solution set is

solution of inequalities

The Solution set is

another solution of inequalities

The solution set of the system (Figure 5.8) is

system of inequalities

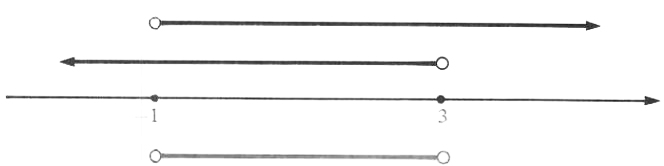
graphical representation for solution set example

FIGURE 5.8

Let's see how our Linear inequalities solvergenerates graph for this and similar problems. Click on "Solve Similar" button to see more examples.

Solution of Linear Equations with Absolute Values

The absolute value of a numberA ∈ R, denoted by|a|, is either+a or-a whichever is positive, and is zero ifa=0

That is,

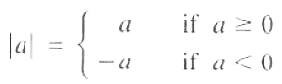
absolute value

EXAMPLES 1. |6|=6

2. |-4|=-(-4)=4

 Note that the absolute value of any real number is either zero or a positive number, never a negative number. That is,|a|>=0 for all a∈R.

 When we have the absolute value of a quantity involving a variable such as |x -1| that quantity, x-1. could be

1. greater than or equal to zero, or

2. less than zero.

When x-1 is greater than or equal to zero, that is,

x-1>=0

then |x -1| = x-1

When x-1 is less than zero, that is, x-1<0, then

|x -1| = -(x-1) = -x+1

The following examples illustrate how to solve a linear equation in one variable involving absolute value.

EXAMPLE Solve the equation |x -3| = 5

SolutionTo find the solution set of this equation, we have to consider two cases

First

Whenx-3>=0 that is,x>=3

|x -3| = x-3

  The equation now becomes

|x -3| = x-3 = 5 or x=8

  The solution set is the intersection of the solution sets of

x>=3 andx=8

  The solution set (Figure 5.9) is {8}.

Another example of intersection of Solution set derived from graphical representation

  Figure 5.9

Second When x-3<0 that is, x<3

|x -3| = -(x-3) = -x+3

  The equation now becomes

|x -3| = -x+3 = 5 or x = -2

  The solution set is the intersection of the solution sets of

x<3 and x=-2

  The solution set (Figure 5.10) is {-2}.

example of intersection of Solution set derived from graphical representation

  Figure 5.10

  The solution set of |x -3| = 5 is the union of the solution sets in the tow case

  Hence the solution set is {-2, 8}.

EXAMPLE Find the solution of |2x+3| = 9.

Solution First:

  When2x+3>=0 that isx>=-(3/2)

|2x+3| = 2x+3

The equation now becomes

|2x+3| = 2x+3 = 9, or x=3

 The solution set is the intersection of the solution sets of

x>=-(3/2) andx=3

 The solution set (Figure 5.11) is {3}.

Another example of Solution set derived from graphical representation

Figure 5.11

Second: When 2x+3<0, that is, x<-3/2

|2x+3| = -(-2x+3) = -2x-3

The equation now becomes

|2x+3| = -2x-3 = 9, or x=-6

 The solution set is the intersection of the solution sets of

x<-3/2 and x=-6

The solution set (Figure 5.12) is {-6}.

Solution set derived from graphical representation

Figure 5.12

 The solution set of |2x+3| = 6 is the union of the solution sets in the tow case

  Hence the solution set is {-6, 3}.

Note Since the absolute value of any real number is never negative. the solution set of the equation|3x+5|=-4 is Φ

Find the solution set of|2x-5|=x+3.

First

       When2x-5>=0 that isx>=5/2 (1)

Then |2x-5| = 2x-5

Thus|2x-5| = x+3 becomes

2x-5 = x+3, or x=8 (2)

From (1) and (2) the solution set is {8}.

Second   When 2x-5<0, that is, x<5/2; (3)

then|2x-5| = -(2x-5) = -2x+5

Thus, |2x-5| = x+3 becomes

-2x+5 = x+3, or x=2/3 (4)

From (3) and (4) the solution set is {2/3}.

  The solution set of |2x-5| = x+3 is the union of the solution sets in the tow case

  Hence the solution set is {2/3, 8}.

EXAMPLE Find the solution set of|4-3x| = 3x-4.

Solution First

When4-3x>=0 that is,x>=4/3 (1)

then|4-3x| = 4-3x

Thus|4-3x| = 3x-4 becomes

4-3x = 3x-4, or x=4-3 (2)

From (1) and (2) the solution set is {4/3}.

Second   When 4-3x<0, that is x>4/3; (3)

then|4-3x| = -(4-3x) = -4+3x

Thus|4-3x| = 3x-4 becomes

-4+3x = 3x-4 or 0x=0

Which is true for all x ∈ R (4)

From (3) and (4) the solution set is {x|x>4/3}.

 The solution set of |4-3x| = 3x-4 is the union of the solution sets in the tow case

Hence the solution set is

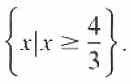
Solution set for union of solution set

Let's see how our Linear equations solver solves for this and similar problems. Click on "Solve Similar" button to see more examples.

Find the Solution Set for the Following Equation

Source: https://quickmath.com/math-tutorials/solution-of-systems-of-linear-inequalities-in-one-variable.html